贪心算法
思想
在每一步都做出在当前看来最好的选择,以求解最优解
- 将问题分解为若干个子问题
- 对每一个子问题,选择代价最小的解决方案,
全局最优解依赖于每个子问题的局部最优解 - 最后得到全局最优解
例题
盛最多水的容器
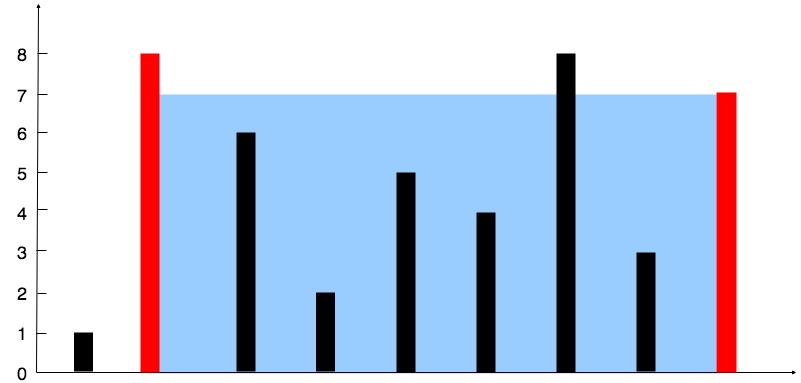
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水
js
const maxArea = function (H) {
let ans = 0
let i = 0; let j = H.length - 1
while (i < j) {
ans = Math.max(ans, Math.min(H[i], H[j]) * (j - i))
H[i] <= H[j] ? i++ : j--
}
return ans
}const maxArea = function (H) {
let ans = 0
let i = 0; let j = H.length - 1
while (i < j) {
ans = Math.max(ans, Math.min(H[i], H[j]) * (j - i))
H[i] <= H[j] ? i++ : j--
}
return ans
}柃檬水找零
在柠檬水摊上,每一杯柠檬水的售价为 5 美元,每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false
js
const lemonadeChange = function (bills) {
const change = { 5: 0, 10: 0 }
for (const bill of bills) {
if (bill === 5) {
change[5]++
}
else if (bill === 10) {
if (!change[5])
return false
change[10]++
change[5]--
}
else {
if (change[5] && change[10]) {
// 5元是万能解,优先使用10元
change[10]--
change[5]--
}
else if (change[5] >= 3) {
change[5] -= 3
}
else {
return false
}
}
}
return true
}const lemonadeChange = function (bills) {
const change = { 5: 0, 10: 0 }
for (const bill of bills) {
if (bill === 5) {
change[5]++
}
else if (bill === 10) {
if (!change[5])
return false
change[10]++
change[5]--
}
else {
if (change[5] && change[10]) {
// 5元是万能解,优先使用10元
change[10]--
change[5]--
}
else if (change[5] >= 3) {
change[5] -= 3
}
else {
return false
}
}
}
return true
}